28.找出字符串中第一个匹配项的下标

难度：容易

给你两个字符串 s 和 p ，请你在 s 字符串中找出 p 字符串的第一个匹配项的下标（下标从 0 开始）。如果 p 不是 s 的一部分，则返回 -1 。

示例 1：

输入：s = "sadbutsad", p = "sad"
输出：0
解释："sad" 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ，所以返回 0 。

示例 2：

输入：s = "leet-code", p = "leeto"
输出：-1
解释："leeto" 没有在 "leet-code" 中出现，所以返回 -1 。

提示：

• 1 <= s.length, p.length <= 104
• s 和 p 仅由小写英文字符组成

解题思路（暴力匹配）

设置两个指针 i 和 j，都初始化为 0，我们对比 s 在 i 位置，p 在 j 位置的字符。

如果 s[i] == p[j]，那么 i 和 j 都移到下一个位置。

否则 j 回退到 0，i 回退到 1，继续上述过程，如果在下一次比较中，还是出现了不匹配的字符，那么 j 回退到 0，i 回退到 2，继续……，周而复始。

直到某一次匹配中，如果 j 到达越界位置，那么 s 包含 p，否则 s 不包含 p。

我的代码

public int strStr(String s, String p) {
    int ls = s.length();
    int lp = p.length();
    int i = 0;
    int j = 0;
    while (i + lp <= ls) {
        int x = i;
        while (x < ls && j < lp && s.charAt(x) == p.charAt(j)) { // 若当前字符匹配成功
            x++;
            j++;
        }
        if (j == lp) { // 当前子串匹配成功
            return i;
        } else if (j != lp) { // 当前子串匹配失败
            i++;
            j = 0;
        }
    }
    return -1;
}

时间复杂度: O(n × m)，其中 n 是字符串 s 的长度，m 是字符串 p 的长度。最坏情况下我们需要将字符串 p 与字符串 s 的所有长度为 m 的子串均匹配一次。

空间复杂度: O(1)

KMP 算法

KMP 算法是一个用来 快速在原字符串中找到匹配字符串 的算法。

此算法是由 Knuth，Morris 和 Pratt 这三位学者发明的，所以命名采用了他们名字的首字母 KMP。

上述的暴力匹配解法，最坏的情况下时间复杂度为 O(m ∗ n) ，而 KMP 算法的复杂度为 O(m + n)。

KMP 之所以能够在 O(m+n) 复杂度内完成查找，是因为其能在 非完全匹配 的情况下提取到 有效信息 进行 再次利用，以减少 重复匹配 的行为。

这么说似乎有点抽象，让我们从暴力匹配法存在的问题开始讲起。

暴力匹配法的不足

上面的暴力方法是基于这样的一个尝试的思路：

如果 s 中有一个子串和 p 是匹配的，因为任何一个子串都有一个 开头位置，那么这个和 p 匹配的子串当然也有一个 开头位置，又因为我们不知道哪个 开头位置 的子串和 p 是匹配的，因此我们尝试所有可能的开头。如果我们尝试完所有的 开头位置，都没有发现一个子串可以和 p 匹配，那么 s 中就没有一个子串和匹配，即 s 不包含 p，反之 s 包含 p。那么这个过程它为什么低效呢？我们来看一下 s = "aaaaaaaaab" 和 p = "aaab" 的匹配过程。

我们首先从开头为 0 的子串尝试，当我们发现 s[3] 和 p[3] 不匹配的时候，这说明什么？这只能说明 s 从 0 位置开始的子串不可能和 p 匹配了。

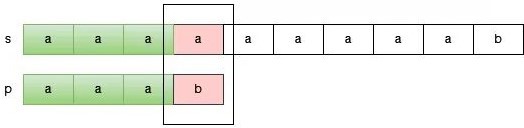
于是，我们只能放弃之前已经匹配的部分，选择下一个开始的位置，继续进行匹配。

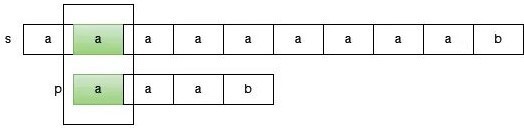
当我们发现某一个开头的尝试已经宣告失败的时候，此时只能选择下一个开头，继续从头开始匹配。那么此时指向 s 的指针会回退，之前已经匹配的部分结果完全抛弃，从新开始，因此这个方法是低效的。

改进思路

如果某一次尝试失败了，那么之前已经匹配的部分（之前做过的努力）能否给我们提供一些帮助，加速我们的匹配过程，甚至能使得字符串 s 上的指针不回退呢？我们调整的时候，需要遵循什么原则呢？

如果要保证指针 i 不回退，那么此时我们需要调整指针 j 的位置，使得 s[i] 可以和 p[j] 继续比较。那么把指针 j 调整到哪就是一个值得思考的问题。

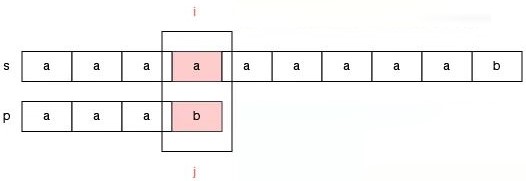
我们调整指针 j 要保证以下几个原则：

1. 毫无疑问，指针 j 一定要前移
2. 指针 j 调整以后，s[i] 和 p[j] 要继续比较，那么一定要保证 s[i] 和 p[j] 之前的部分（如果有的话）是匹配的，这是因为 i 不回退，如果之前的部分是不匹配的，那么后续的比较就是没有意义的
3. 指针 j 调整以后，不能使我们漏掉可能的答案

为了便于说明 j 的调整，下面我们举一个明显的例子。请看字符串 s = "acacab"，和字符串 p = "acab" 的匹配过程。

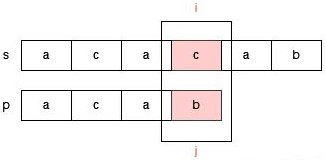
此时 s[i] 和 p[j] 不匹配了，那么我们需要调整指针 j ，我们可以把指针 j 调整到 p[2] 的位置吗？显然是不可以的，因为指针 j 到 p[2] 位置时，s[1,2] 和 p[0,1] 是不匹配的。

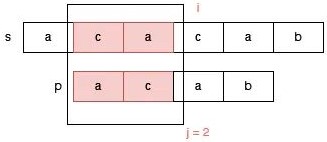
那么应该如何调整指针 j 的位置呢？我们知道，j 指向 p[3] 时 s[0,2] 和 p[0,2] 是匹配的，匹配的这一部分 aca 的前缀 a 和后缀 a 是匹配的，因此我们可以把指针 j 调整为指向 p[1]：

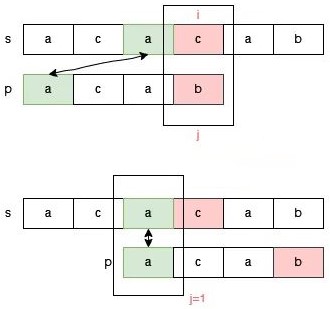
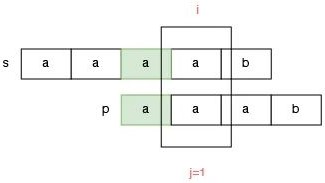
如果已经匹配的部分有多个前缀和后缀是匹配的情况，我们该怎么选择？请看 s = "aaaab" 和 p = "aaab" 的匹配过程。

此时已经匹配的部分是 aaa，那么这个字符串有两组前后缀匹配的情况，一种是前缀 a 和后缀 a 是匹配的：

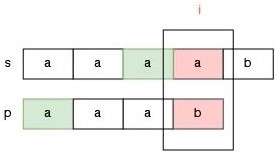
还有一种情况是前缀 aa 和后缀 aa 匹配：

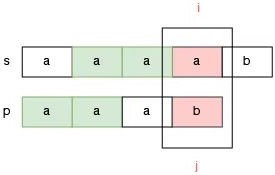
那么怎么选择呢？答案是：选择最长的前后缀匹配，否则可能会漏掉可能的答案。

例如，如果选择前后缀匹配长度为 1 的部分，那么指针 j 应该调整为 p[1]，此时我们得到的答案是：aaaab 不包含 aaab，因为指针 i 会提前到越界位置，但是 aaaab 不包含 aaab 显而易见是错误的答案。

如果选择前后缀匹配长度为 2 的部分，那么指针 j 应该调整到 p[2] 的位置，这样，我们就没有漏掉这个可能的答案：

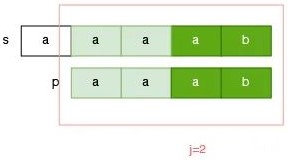
**总结一下：**此时我们似乎找到了，保证 s 指针不回退的时候，p 的指针的调整方案，即当我们发现某一次匹配失败的时候，我们需要找出前面已经匹配部分的 前后缀最大匹配长度，假设为 next，那么我们只需要把指针 j 调整为指向 p[next]，继续进行匹配操作即可。

next 数组

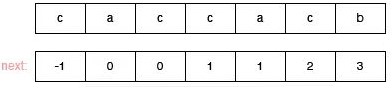
我们在进行真正的匹配之前，我们要先计算好，模式串 p 每一个元素的 next 值（next 值的含义就是当前元素不匹配的时候，它前面部分字符串的前后缀最大匹配长度，这个前后缀不包含自己），看下面对模式串 caccacb 的 next 值的定义过程：

• 0 位置前面没有字符串了，它不存在 next 的值的概念因此这位置的 next 值是人为规定的，我们设定它是 -1 ，是多少都无所谓。
• 1 位置前面的字符串只有一个字符 c，而前后缀不能包含自身，因此 1 位置的 next 值就是 0。
• 2 位置前面的字符串是 ac，它的前后缀里没有匹配的，因此这个位置的 next 值是 0。
• 3 位置前面的字符串是 cac，它的能够匹配的最长前后缀是 c，因此 3 位置的 next 值是 1。
• 4 位置前面的字符串是 cacc，它的能够匹配的最长前后缀是 c，因此 4 位置的 next 值是 1。
• 5 位置前面的字符串是 cacca，它的能够匹配的最长前后缀是 ca，因此 5 位置的 next 值是 2。
• 6 位置前面的字符中是 caccac，它的能够匹配的最长前后缀是 cac，因此 6 位置的 next 值是 3。

使用 next 数组加速匹配过程

如果我们在开始匹配之前，先得到了一个关于模式 p 的每一个位置 index 不匹配后，模式串的匹配指针应该调整为 next[index] 的 next 数组的话，那么我们的匹配过程可以变成这样：

public int strStr(String s, String p) {
    int ls = s.length();
    int lp = p.length();
    int[] next = getNext(p);// 获取关于模式串 p 的 next 数组
    int i = 0;
    int j = 0;
    while (i <= ls) {// 注意边界条件
        if (i < ls && j < lp && s.charAt(i) == p.charAt(j)) {// 若当前字符匹配成功，但子串还未匹配完全
            i++;
            j++;
        } else if (j == lp) {// 若当前子串匹配成功
            return i - lp;
        } else if (j == 0) {// 如果模式串p的第一个字符p[0]和字符串s的当前字符s[i]都不匹配，
            				// 那么说明s中从i开始不可能匹配出p来，因此换下一个开头继续尝试
            i++;
        } else if (j != 0) {// 如果j位置不是0，说明它前面有匹配成功的部分，
                            // 那么此时j应该调整为next[j]的位置
            j = next[j];
        }
    }
    return -1;
}

next 数组能加速匹配过程，可以从下面两个方面来理解：

• 保证 i 指针不回退，指导 j 指针的调整：在我们匹配失败的时候，它可以利用我们之前已经匹配的部分字符串（以前做过的努力），在保证指针 i 不回退的情况下，指导此时指针 j 应该做怎样的调整。

• 跳过了一些无需验证的可能性：在暴力做法中，我们尝试字符串 s 中每一个可能的开头位置（即验证所有的可能性），而 next 数组指导指针 j 的调整，可以跳过一些根本不可能匹配出来模式串 p 的位置。

这两种理解是等价的。

next 数组的正确性分析

我们举一个例子说明 next 数组能够指导 j 指针的调整，同时保证 i 指针不回退，并且还能跳过那些不可能的开头位置。

如下图字符串 s = "caccacb" 和字符串 p = "cacb" 的匹配过程所示。

此时我们正在尝试在 s 中从 0 位置开始的字符能否匹配出字符串 p，此时由于 s[3] != p[3]，于是根据 next[3] = 1，于是我们调整 j = 1：

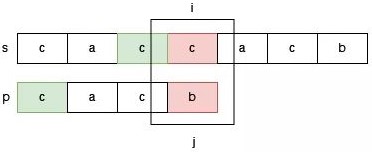
当我们把 j 调整为 1 的时候，此时 p[0] 和 s[2] 对齐，我们在探索 s 中从 2 位置开始的字符串能否匹配出来 p，它直接跳过了 s 中 1 位置开始的字符串能否匹配出 p 的可能性。

为什么能跳过，因为 next 数组的 最长匹配前后缀长度 告诉我们 s 中 1 位置开始的字符串不可能匹配出来 p，即跳过的位置都是不可能匹配出 p 的位置。

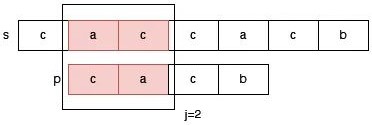
为了更好的理解 next 数组的加速原理，我们可以尝试匹配一下 s 中的 1 位置开始的字符串，如下图所示。此时 j 需要调整为 2。我们可以看到，j 前面的部分 p[0,1] 和 s[1,2] 已经是不匹配的了。因此我们完全不用在意 j 调整为 next[j] 的时候所跳过的位置，因为这些位置根本不会匹配出来模式串 p。

构造 next 数组

在字符串 p 中，假设 i 位置以前的 next 值都求解好了，现在需要求解 i 位置的 next 值，假设 next[i - 1] = m，也就是 p[0,m-1] 和 p[i-m-1,i-2] 相互匹配：

首先提问，next[i] 有没有可能超过 m + 1 呢？答案是不可能。

假设 next[i] = k，且k > m + 1，那么必然存在一个长度为 k 的前缀 p[0…k-1]，和后缀 p[i-k,i-1] 是匹配的，那么 p[0,k-2] 和 p[i-k,i-2] 也是匹配的，即 next[i - 1] 可以达到 k - 1。

而 k - 1 是大于 m 的，和假设 next[i - 1] = m 矛盾，因此 next[i] 不会超过 m + 1 ，即 next[i] <= m + 1。

得到这个前提的情况下，我们考察 p[m] 和 p[i - 1] 的关系：

• 第一种情况，p[m] == p[i-1]

  

  此时 p[0,i-1] 中可以 继承 得到一个更长的匹配前缀 p[0,m] 和后缀 p[i-m-1,i-1]，显然 next[i] 至少是 m + 1 ，即 next[i] >= m + 1。

  根据上述得到的前提 next[i] <= m + 1，可知此时 next[i] = m + 1。

• 第二种情况，p[m] != p[i-1]

  

  根据上述得到的前提 next[i] <= m + 1，此时显然 next[i] 也不会等于 m + 1 了，也就是无法 继承 p[0,m] 中的最长相同前后缀了。

  但这不代表 next[i] 的值就是 0 了。

  而是我们需要在p[0,m-1] 范围内找到一个p[0,n]，看看能否和 p[i-n-1,i-1] 匹配，此时 0 <= n <= m。

  我们把 p[0,m] 这部分当成模式串 p，把 p[i-m-1,i-1] 当成我们前面字符串模式匹配问题中的 s 字符串，此时不就是关于某一次匹配失败的时候，字符串 s 的匹配指针不回退，如何调整模式串的匹配指针的问题吗？

  那么我们此时让 p[i-1] 和 p[next(m)] 比较即可，匹配失败的时候，我们把 m 调整成 next[m]

  

next 数组的代码实现

public int[] getNext(String p) {
    // 构建 next 数组，数组长度为匹配串的长度（next 数组是和匹配串相关的）
    int lp = p.length();
    int[] next = new int[lp]; 
    next[0] = -1;
    if (lp > 1) {
        next[1] = 0;
        //i: 当前要求解next[i]
        //m: 始终记录next[i - 1]的值
        int i = 2;
        int m = next[i - 1];
        while (i < lp) {
            if (p.charAt(i - 1) == p.charAt(m)) {// p[m] == p[i-1]
                next[i] = m + 1;
                i++;
                m = next[i - 1];
            } else if (m == 0 && p.charAt(i - 1) != p.charAt(m)) {// p[m] != p[i-1]且前后缀没有匹配的可能
                next[i] = 0;
                i++;
            } else if (m != 0 && p.charAt(i - 1) != p.charAt(m)) {// p[m] != p[i-1]但前后缀还有匹配的可能
                m = next[m];
            } 
        }
    }
    return next;
}

这就是整个 next 数组的构建过程，时间复杂度和空间复杂度均为 O(lp)。

KMP 算法的完整代码

public int strStr(String s, String p) {
    int ls = s.length();
    int lp = p.length();
    int[] next = getNext(p);// 获取关于模式串 p 的 next 数组
    int i = 0;
    int j = 0;
    while (i <= ls) {
        if (i < ls && j < lp && s.charAt(i) == p.charAt(j)) {// 若当前字符匹配成功
            i++;
            j++;
        } else if (j == lp) {
            return i - lp;
        } else if (j == 0) {
            i++;
        } else if (j != 0) {
            j = next[j];
        }
    }
    return -1;
}

public int[] getNext(String p) {
    // 构建 next 数组，数组长度为匹配串的长度（next 数组是和匹配串相关的）
    int lp = p.length();
    int[] next = new int[lp];
    next[0] = -1;
    if (lp > 1) {
        next[1] = 0;
        //i: 当前要求解next[i]
        //m: cn始终记录next[i - 1]的值
        int i = 2;
        int m = next[i - 1];
        while (i < lp) {
            if (p.charAt(i - 1) == p.charAt(m)) {// p[m] == p[i-1]
                next[i] = m + 1;
                i++;
                m = next[i - 1];
            } else if (m == 0 && p.charAt(i - 1) != p.charAt(m)) {// p[m] != p[i-1]且前后缀没有匹配的可能
                next[i] = 0;
                i++;
            } else if (m != 0 && p.charAt(i - 1) != p.charAt(m)) {// p[m] != p[i-1]但前后缀还有匹配的可能
                m = next[m];
            } 
        }
    }
    return next;
}

时间复杂度: O(n+m)

空间复杂度: O(m)

总结

KMP 算法的应用范围要比 Manacher 算法广，Manacher 算法只能应用于「回文串」问题，相对比较局限，而「子串匹配」问题还是十分常见的。

背过这样的算法的意义在于：相当于大脑里有了一个时间复杂度为 O(n) 的 api 可以使用，这个 api 传入一个原串和匹配串，返回匹配串在原串的位置。